24392번: 영재의 징검다리
첫 줄에 N과 M(1 ≤ N, M ≤ 1,000)이 공백으로 구분되어 주어지고, 그 뒤에는 N줄에 걸쳐 다리의 정보가 주어진다. 강화유리의 경우 1, 일반 유리의 경우 0으로 주어진다.
www.acmicpc.net
문제 요약
1. 첫 줄에 N과 M, 영재가 건널 수 있는 다리 정보 N*M (1<=N,M<=1,000)이 주어진다.
2. 지도에서 0으로 표시된 일반 유리는 건널 수 없으며, 1로 표시된 강화 유리는 건널 수 있다.
3. 예를들어 N=3, M=5인 경우, 시작점과 도착점, 그리고 영재가 건널 수 있는 경로는 아래와 같다.
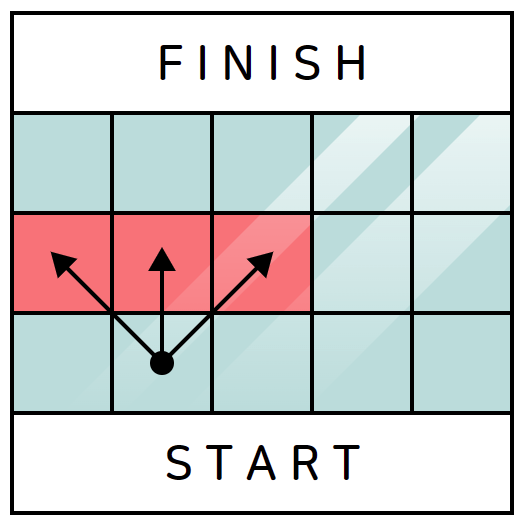
4. 영재가 다리를 건널 수 있는 경우의 수를 1,000,000,007로 나눈 나머지를 출력하라.
핵심 요약
정답을 1,000,000,007로 나눈 나머지를 출력하라고 언급되어 있는게 핵심 포인트다.
보통 이런식의 문제는 십중팔구로 DP(다이나믹 프로그래밍 = 동적 프로그래밍)를 요구한다.
만약 이 문제를 DFS로 접근할 경우, 1000*1000의 지도, 시작지점과 도착지점이 고정적이지 않다는 점, 움직일 수 있는 경로가 3가지라는 특성들때문에 곧 바로 시간초과가 발생한다.
문제 풀이
#include <iostream>
#define TEMP 1000000007
using namespace std;
unsigned long long dp[1000][1000], ans = 0;
int arr[1000][1000], h, w, nx, mx[]={-1,0,1};
void input(){
cin >> h >> w;
for(int i=0; i<h; i++){
for(int j=0; j<w; j++) cin >> arr[i][j];
}
}
int main()
{
input();
for(int i=0; i<w; i++) if(arr[h-1][i]==1) dp[h-1][i] = 1;
for(int i=h-2; i>=0; i--){
for(int j=0; j<w; j++){
if(arr[i][j]==1){
for(int k=0; k<3; k++){
nx = j+mx[k];
if(nx<0||nx>=w) continue;
if(dp[i+1][nx]>0) dp[i][j] += (dp[i+1][nx] % TEMP);
}
}
}
}
for(int i=0; i<w; i++) ans += dp[0][i];
cout << ans % TEMP << "\n";
return 0;
}지도의 맨 아래, 즉, arr[h-1][0] ~ arr[h-1][w-1]의 모든 지점이 시작지점이며, arr[0][0] ~ arr[0][w-1]의 모든 지점이 도착지점이다. 이 점을 유의하고 DP를 구현하면 된다.
추가로 dp의 누적값을 저장하는 배열을 int로 선언할 경우 오답이 발생하니, 이 점만 유의하자.

'🖥️ CS > Baekjoon Algorithms' 카테고리의 다른 글
| 백준 18430번 무기공학 (C++) (0) | 2021.11.01 |
|---|---|
| 백준 6987번 월드컵 (C++) (0) | 2021.10.28 |
| 백준 16508번 전공책 (C++) (0) | 2021.10.22 |
| 백준 19640번 화장실의 규칙 (C++) (0) | 2021.10.15 |
| 백준 9935번 문자열 폭발 (C++) (0) | 2021.10.07 |