문제 링크 : www.acmicpc.net/problem/16931
16931번: 겉넓이 구하기
크기가 N×M인 종이가 있고, 종이는 1×1크기의 칸으로 나누어져 있다. 이 종이의 각 칸 위에 1×1×1 크기의 정육면체를 놓아 3차원 도형을 만들었다. 종이의 각 칸에 놓인 정육면체의 개수가 주어
www.acmicpc.net
간만에 옛날에 배웠던 수학 개념이 나왔다.
겉넓이란 말 그대로 대상의 모든 표면의 넓이를 의미한다.
예를들어 가로 세로 1cm의 정육면체 겉넓이는 6cm이다. 한 면의 넓이가 1이고 모두 6개의 면으로 이루어져있기 때문이다.
직육면체의 겉넓이는 다음과 같은 공식이다.
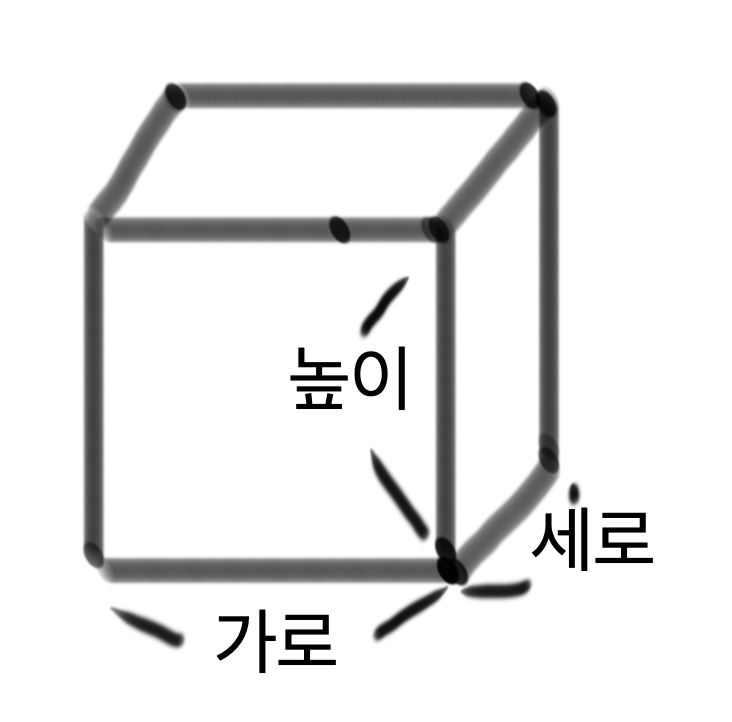
2 * (가로*세로 + 가로*높이 + 세로*높이)
문제 풀이는 간단하다.
한 좌표의 arr[y][x]의 겉넓이를 구하고 그 좌표를 기준으로 둘러싼 4방면과의 겉넓이를 비교한다.
4방면과 비교했을때 비교대상의 높이가 arr[y][x]보다 크다면 arr[y][x]의 겉넓이 - arr[y][x](즉, 높이)를 해준다.
반대로 비교대상의 높이가 arr[y][x]보다 작으면 arr[y][x]의 겉넓이 - 비교대상의 좌표값(즉, 높이)을 해준다.
그렇게 맞닿은 면적들의 값을 빼주고 남은 값을 정답에 더해주면 된다.
#include <iostream>
#define MAX 101
using namespace std;
int arr[MAX][MAX], my[] = {1,0,-1,0}, mx[] = {0,1,0,-1}, ny, nx, y, x, n, m, temp, ans = 0;
void solve(){
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
temp = 2*(1+arr[i][j]+arr[i][j]);
y = i;
x = j;
for(int i=0; i<4; i++){
ny = y+my[i];
nx = x+mx[i];
if(ny>=1&&ny<=n&&nx>=1&&nx<=m){
if(arr[y][x]>=arr[ny][nx]) temp -= arr[ny][nx];
else temp -= arr[y][x];
}
}
ans+=temp;
}
}
}
void input(){
cin >> n >> m;
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++) cin >> arr[i][j];
}
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
input();
solve();
cout << ans << "\n";
return 0;
}
'🖥️ CS > Baekjoon Algorithms' 카테고리의 다른 글
| 백준 12946번 육각 보드 (C++) (0) | 2021.05.10 |
|---|---|
| 백준 1806번 부분합 (C++) (0) | 2021.05.06 |
| 백준 2636번 치즈 (C++) (0) | 2021.05.03 |
| 백준 16234번 인구이동 (C++) (0) | 2021.05.02 |
| 백준 2217번 로프 (C++) (0) | 2021.04.30 |