문제 링크 : www.acmicpc.net/problem/13023
13023번: ABCDE
문제의 조건에 맞는 A, B, C, D, E가 존재하면 1을 없으면 0을 출력한다.
www.acmicpc.net
문제 풀이는 다음과 같다.
1. 먼저 다음과 같은 배열들을 생성한다.
(1) 2차원 bool문 배열 (입접행렬 : 서로 연결이 되어있는지 아닌지를 판단)
(2) 2차원 int형 벡터 (입접리스트 : 연결된 *노드들을 저장)
(3) pair int형 벡터 (간선리스트 : 연결된 *간선들을 저장)
*노드(N) : 그래프의 정점
*간선(E) : 그래프의 간선 (선분, 연결선)
2. n과 m을 입력받고 m의 크기만큼 시작지점과 끝지점을 입력 받는다.
친구관계로 저장받지만, 편의상 나는 시작지점과 끝지점이라고 명하겠다. 입력받는 값들은 아래와 같다.
cin >> from >> to;
ch[from][to] = ch[to][from] = true; // 양쪽 모두 친구니까!
node[from].push_back(to); // 양쪽 모두 친구니까!
node[to].push_back(from); // 양쪽 모두 친구니까!
edge.push_back({from,to}); // 양쪽 모두 친구니까!
edge.push_back({to,from}); // 양쪽 모두 친구니까!양쪽 모두 친구니까! 라는 뜻은, 결국 양방향이라는 말과 동일하다.
3. 이제부터 A->B->C->D->E의 친구관계가 성립되는지 판단할거다.
for문을 써서 친구관계를 판단하기 이전에, m을 2배로 증가시켜주자.
양방향 간선들을 저장시켰으므로, 결국 m의 값은 2배로 증가할 수 밖에 없다.
m*=2;
4.2중 for문을 돌려서 모든 간선들의 연관성을 테스트한다.
for(int i=0; i<m; i++){
for(int j=0; j<m; j++){
if(i==j) continue;
A=edge[i].first;
B=edge[i].second;
C=edge[j].first;
D=edge[j].second;
if(A==B||A==C||A==D||B==C||B==D||C==D) continue;
if(!ch[B][C]) continue;
. . . (생략)
}i와j가 같은 경우는 판단할 필요가 없으나 곧 바로 패스한다.
위 코드를 그림으로 표기하면 아래와 같다.
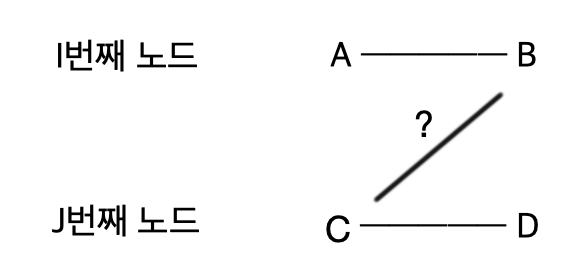
A와 B가 친구이고 C와 D가 친구인것까지는 알겠다.
하지만 만약 A,B,C,D중 서로 동일한 인물이 섞일 경우, 즉, 아래 코드가 성립될 경우 위 그림이 성립되지 않으므로 곧 바로 패스한다.
if(A==B||A==C||A==D||B==C||B==D||C==D) continue;또한 저 이미지에서 A->B->C->D가 성립되는 것을 판단하라면 B와 C가 서로 연결되어있어야 하는데, 이는 아래 코드가 성립되는지를 판단해서 알 수 있다.
if(!ch[B][C]) continue;
5. 아래 코드는 위 코드에서 (생략)으로 표시된 부분이다.
for(int x=0; x<node[D].size(); x++){
E=node[D][x];
if(E==A||E==B||E==C||E==D) continue;
cout << 1 << "\n";
return 0;
}이제 A->B->C->D까지의 관계를 알아냈으니, D->E만 알아내면 된다.
D에 연결된 노드 중에서 A,B,C,D와 동일하지 않은 노드가 있을 경우, 결국 A->B->C->D->E가 성립되므로 1을 출력하고 종료하면 된다.
#include <iostream>
#include <vector>
#include <algorithm>
#define MAX 2001
using namespace std;
bool ch[MAX][MAX];
vector<int> node[MAX];
vector<pair<int,int>> edge;
int main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
int n,m,from,to,A,B,C,D,E;
cin >> n >> m;
for(int i=0; i<m; i++){
cin >> from >> to;
ch[from][to] = ch[to][from] = true;
node[from].push_back(to);
node[to].push_back(from);
edge.push_back({from,to});
edge.push_back({to,from});
}
m*=2;
for(int i=0; i<m; i++){
for(int j=0; j<m; j++){
if(i==j) continue;
A=edge[i].first;
B=edge[i].second;
C=edge[j].first;
D=edge[j].second;
if(A==B||A==C||A==D||B==C||B==D||C==D) continue;
if(!ch[B][C]) continue;
for(int x=0; x<node[D].size(); x++){
E=node[D][x];
if(E==A||E==B||E==C||E==D) continue;
cout << 1 << "\n";
return 0;
}
}
}
cout << 0 << "\n";
return 0;
}
'🖥️ CS > Baekjoon Algorithms' 카테고리의 다른 글
| 백준 2615번 오목 (C++) (0) | 2021.04.14 |
|---|---|
| 백준 16929번 Two Dots (C++) (0) | 2021.04.13 |
| 백준 13398번 연속합 2 (C++) (0) | 2021.04.10 |
| 백준 11054번 가장 긴 바이토닉 부분 수열 (C++) (0) | 2021.04.10 |
| 백준 11055번 가장 큰 증가 부분 수열 (C++) (0) | 2021.04.10 |