🖥️ CS/Data Structure & Algorithm
동적 계획법 (Dynamic Programming)
한국의 메타몽
2020. 4. 22. 12:44
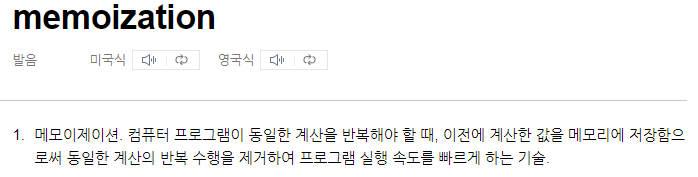
동적계획법 (Dynamic Programmign) = Memoization(메모이제이션)
한줄 요약을 하자면, 기존에 구했던 답을 재활용해서 불필요한 연산은 배제하는 계산법이다.
연산의 효율성을 위해 여러 문제를 나눠서 풀고, 이 과정에서 이미 구한 답을 활용해 불필요한 계산식은 배제한다.
피보나치수열 - (일반 재귀풀이)
#include <iostream>
using namespace std;
int Fibo(int x){
int total = 0;
if(x<=1){
total = x;
}
else if(x>=2){
total+=Fibo(x-2)+Fibo(x-1);
}
return total;
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t;
cin >> t;
cout << Fibo(t) << "\n";
return 0;
}
예를들어 재귀로 피보나치 문제를 풀면, 일일이 재귀를 호출하다보니 계산량이 많아질 수 밖에 없다.
기존의 재귀문제로 피보나치 수열 100을 구해보면 2^100이라는 어마무시한 연산량이 나오게된다.
이를 위해 동적계획법(DP)을 사용하면 중복된 계산식을 활용하지 않고도 이미 계산된 값을 활용해 답을 구할 수 있다.
기존의 재귀가 아닌 동적계획(DP)으로 풀면 아래와 같다.
1. 재귀함수를 통한 동적계획법
#include <iostream>
using namespace std;
unsigned long long fibo[91];
unsigned long long calculate(int x){
if(x<=1) return x;
else if(fibo[x]) return fibo[x];
return fibo[x] = calculate(x-1) + calculate(x-2);
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t;
cin >> t;
cout << calculate(t);
return 0;
}2. For문을 통한 동적계획법
#include <iostream>
using namespace std;
unsigned long long fibo[91];
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t;
cin >> t;
fibo[0] = 0; fibo[1] = 1;
for(int i=2; i<=t; i++) fibo[i] = fibo[i-1] + fibo[i-2];
cout << fibo[t];
return 0;
}
출처 : https://blog.naver.com/kdr06006/221736564691
동적계획법(Dynamic Programming)
안녕하세요.오늘은 동적계획법을 하겠습니다.메모이제이션이라고도 합니다.대회에서 아주 잘 나오는 유형 ...
blog.naver.com