백준 2146번 다리 만들기 (C++)
문제 링크 : www.acmicpc.net/problem/2146
2146번: 다리 만들기
여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은 섬을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다
www.acmicpc.net
BFS를 활용해서 풀 수 있는 문제다.
문제를 풀기 전에, 먼저 고민해야할 영역은 다음과 같다.
1. 섬과 섬을 구분하는 방법
-> 여러가지 방법이 있겠지만, 나는 각 섬마다 모두 똑같은 1이 아닌 고유의 값을 가지게 해서 구분했다.
예를들어 어떤 섬은 2의 값만 가지게 하고, 어떤 섬은 3의 값만 가지게 하는 방식이다.
2. 섬과 섬의 최단 거리를 계산하는 방법
-> 문제를 유심히 지켜보니 섬과 섬의 최단 거리 공식은 결국 다음과 같은 결론이 나왔다.
(절대값)세로의 길이차 + (절대값)가로의 길이차 - 1
문제 풀이는 다음과 같다.
1. 아래 코드는 섬과 바다의 값을 입력 받는 코드이다.
void input(){
int label = 1;
cin >> n;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
cin >> arr[i][j];
if(arr[i][j]!=0) arr[i][j] = -1;
}
}
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(arr[i][j]<0){
label_land(i,j,label++);
}
}
}
}섬과 바다의 값을 입력 받는다. 이때 섬의 값이 주어질 경우, 해당 섬의 값을 -1로 변경해준다.
모든 값을 입력 받은 후, 섬과 섬을 구분짓는 라벨링 작업을 시작해준다.
라벨링을 위해 함수 인자로 y의 위치, x의 위치, 그리고 라벨링 숫자를 넘겨 받는다.
라벨링 넘버는 1부터 시작해서 점점 증가하는 구조이다.
2. 아래는 섬을 라벨링 하는 코드이다.
void label_land(int y, int x, int idx){
queue<pair<int,int>> q;
q.push({y,x});
while(!q.empty()){
bool edge = false;
yy = q.front().first;
xx = q.front().second;
arr[yy][xx] = idx;
q.pop();
for(int i=0; i<4; i++){
ny = yy + my[i];
nx = xx + mx[i];
if(ny>0&&ny<=n&&nx>0&&nx<=n&&arr[ny][nx]<0){
arr[ny][nx] = idx;
q.push({ny,nx});
}
else if(ny>0&&ny<=n&&nx>0&&nx<=n&&arr[ny][nx]==0) edge = true;
}
if(edge) v.push_back({yy,xx});
}
}전형적인 BFS 코드이다. 섬일 경우 라벨링의 숫자로 값을 저장하면 된다.
이때 눈여겨봐야할 점이 있는데, 만약 섬의 4방향 중 단 하나의 값이라도 0이 나올 경우, 해당 섬은 결국 섬의 모서리, 즉, 외곽지점임을 뜻한다. 이럴 경우 다리를 연결할 수 있는 지점이 될 수 있음을 뜻하므로, 벡터에 별도로 저장해준다.
+ 엄밀히 말하자면 4방향 중 단 하나의 값이 0이 나온다고 무조건 섬의 모서리라는 뜻은 아니다.
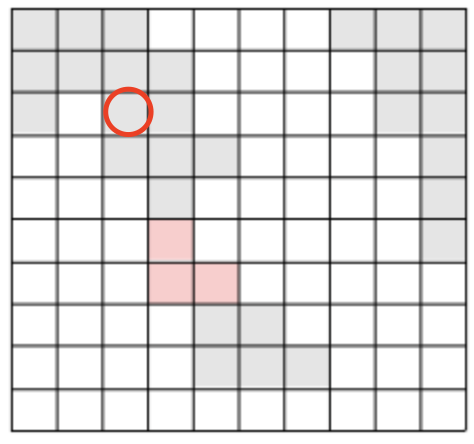
위의 붉은 동그라미는 섬의 모서리가 아니지만, 위의 공식을 적용하면 왼쪽이 바다인 관계로 섬의 모서리로 분류된다.
하지만 상관없다. 저런 값을 넣어줘도 결국 최단거리의 값은 따로 나올 수 밖에 없다.
3. 섬의 모서리를 모두 저장했으면 이제 섬과 섬 사이의 최단 거리를 구해준다.
이때 정답 변수 ans의 최대값은 int형 값의 최대값으로 초기화 시켜주는 것을 잊으면 안된다.
void distance_circulate(){
int temp = 0;
for(int i=0; i<v.size()-1; i++){
yy = v[i].first;
xx = v[i].second;
for(int j=i+1; j<v.size(); j++){
ny = v[j].first;
nx = v[j].second;
if(arr[yy][xx]>0&&arr[ny][nx]>0&&arr[yy][xx]!=arr[ny][nx]){
temp = abs(yy-ny)+abs(xx-nx)-1;
if(ans>temp) ans = temp;
}
}
}
}위에도 언급했지만, 결국 최단 거리를 구하는 공식은 아래로 귀결된다.
(절대값)세로의 길이차 + (절대값)가로의 길이차 - 1
4. 답을 출력한다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#define MAX 101
using namespace std;
int arr[MAX][MAX], n = 0, ans = 1e9, my[] = {1,-1,0,0}, mx[] = {0,0,1,-1}, ny, nx, yy, xx;
vector<pair<int,int>> v;
void distance_circulate(){
int temp = 0;
for(int i=0; i<v.size()-1; i++){
yy = v[i].first;
xx = v[i].second;
for(int j=i+1; j<v.size(); j++){
ny = v[j].first;
nx = v[j].second;
if(arr[yy][xx]>0&&arr[ny][nx]>0&&arr[yy][xx]!=arr[ny][nx]){
temp = abs(yy-ny)+abs(xx-nx)-1;
if(ans>temp) ans = temp;
}
}
}
}
void label_land(int y, int x, int idx){
queue<pair<int,int>> q;
q.push({y,x});
while(!q.empty()){
bool edge = false;
yy = q.front().first;
xx = q.front().second;
arr[yy][xx] = idx;
q.pop();
for(int i=0; i<4; i++){
ny = yy + my[i];
nx = xx + mx[i];
if(ny>0&&ny<=n&&nx>0&&nx<=n&&arr[ny][nx]<0){
arr[ny][nx] = idx;
q.push({ny,nx});
}
else if(ny>0&&ny<=n&&nx>0&&nx<=n&&arr[ny][nx]==0) edge = true;
}
if(edge) v.push_back({yy,xx});
}
}
void input(){
int label = 1;
cin >> n;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
cin >> arr[i][j];
if(arr[i][j]!=0) arr[i][j] = -1;
}
}
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(arr[i][j]<0){
label_land(i,j,label++);
}
}
}
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
input();
distance_circulate();
cout << ans << "\n";
return 0;
}
한 번에 답이 나왔던것까지는 좋은데, 아무리봐도 시간복잡도가 너무 크게 잡혔다는게 보였다.
효율적인 코드를 짜기 위해 몇 번의 시도를 거쳤고, 결국 섬의 모서리를 저장하는 방식을 bool문을 활용해 간결하게 작성했다.
그렇게 만들고보니 시간복잡도는 거진 1/11 미만으로 줄어들었다.
참고로 위의 코드는 48ms의 시간 복잡도 코드이다.